
A review of Geometry: tools for a changing world. Point: A point is a location and is named by a capital letter. FM Geometry Vocabulary/Postulates/Theorems. This is the key difference between postulate and theorem. A theorem is a statement that can be proven true.

Difference Between Postulate and Theorem. Theorems – statements that must be proved . So I would write out the definition of a postulate or theorem, and then describe in your own words how it is utilized. Introduction to Geometry – Postulates and Theorems. Angle Addition Postulate – If P is in the . If AB + BC = AC, then B is between A and C. Segment Addition Postulate – If B is between A and C, then AB + BC = AC. Geometry Postulates, Theorems & Relationships. If two parallel lines are cut by a transversal, then. Unit 1 Lesson 2: Postulates and Theorems.
Theorems are proven to be true by making connections between accepted . A theorem is a basic geometric principle which is supported and established by a proof. Connecting Postulates, Definitions, and Theorems.
#Postulates and theorems pdf#
geometry postulates and theorems list with pictures pdf Postulate 8: The measure of an angle is a Definitions, Theorems, Properties, & Postulates Correct . Postulates are … geometry postulates and theorems list with pictures pdf (L7IZHL).

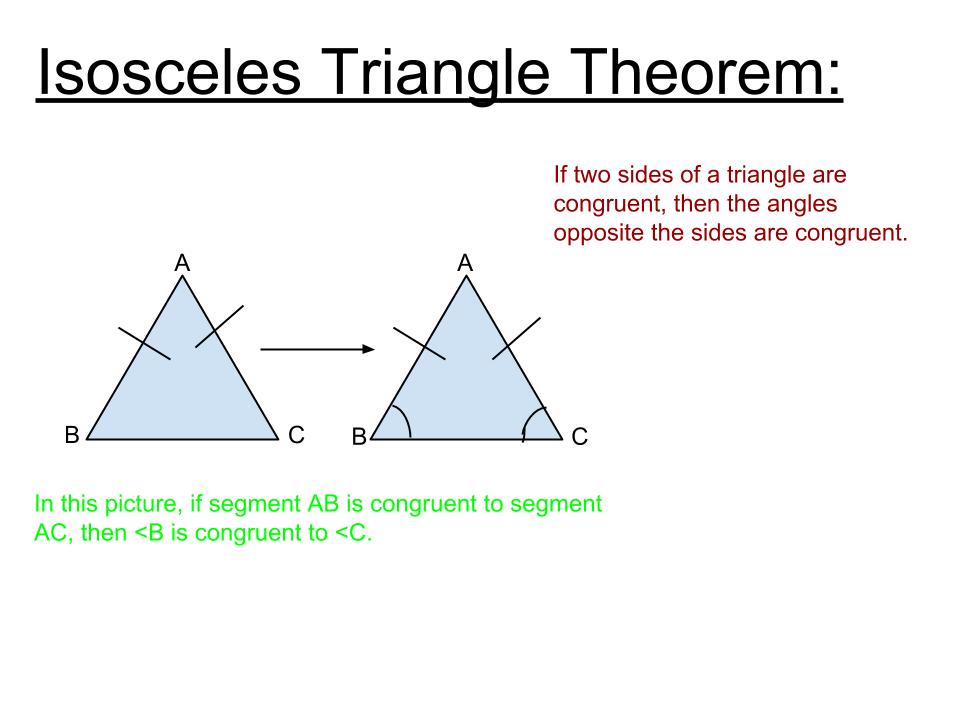
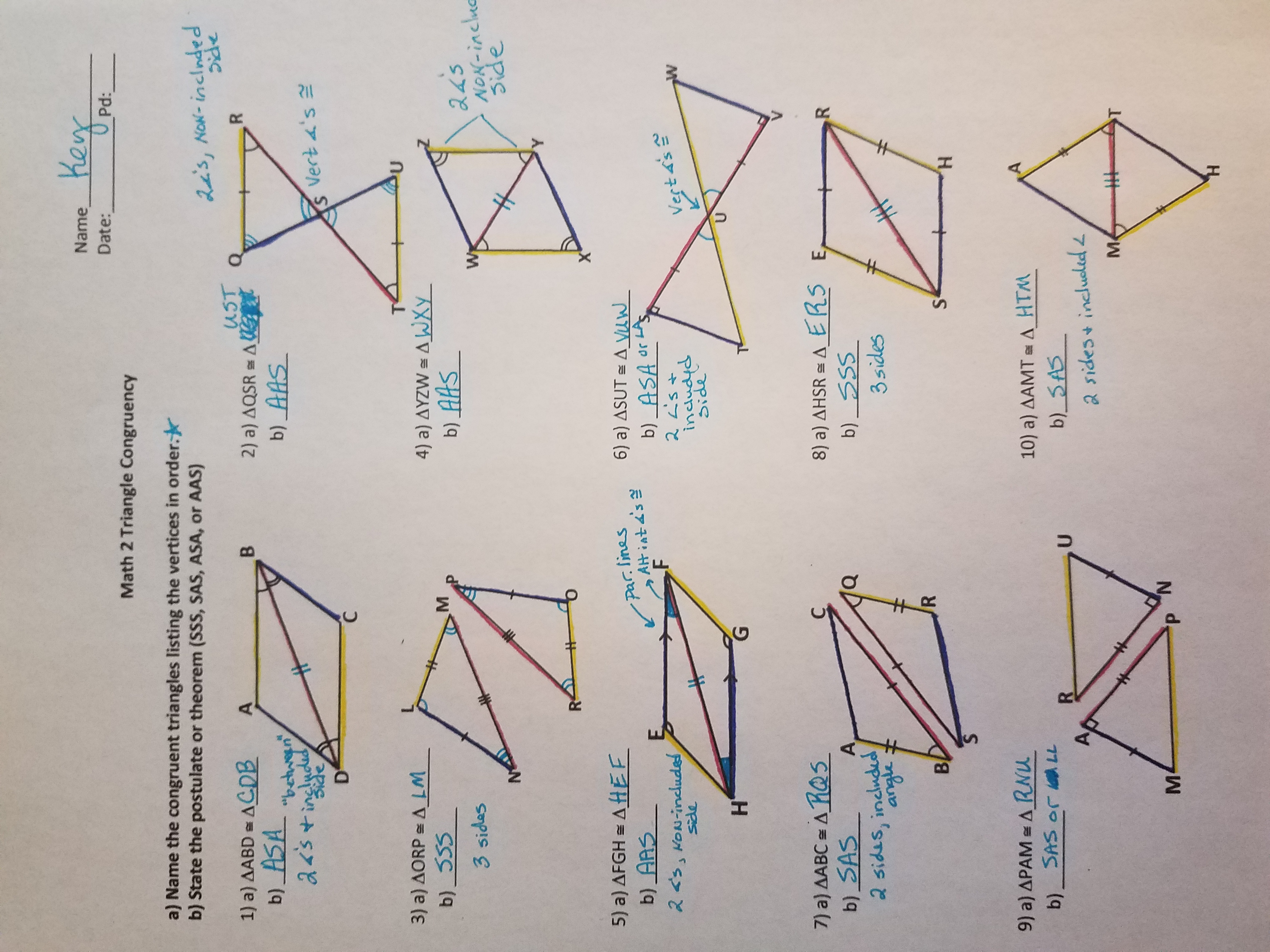
Postulates are the mathematical statements we assume to be true without any proof while theorems are. Difference Between Postulates and Theorems Definition. Postulate 1: A line contains at … What is the Difference Between Postulates and Theorems. Listed below are six postulates and the theorems that can be proven from these postulates. A theorem is a true statement that can be proven. Postulates and Theorems A postulate is a statement that is assumed true without proof. He also shows that AAA is only good for similarity. Sal introduces and justifies the SSS, SAS, ASA and AAS postulates for congruent triangles. To learn more about how we help parents and students in Vancouver visit: Tutoring in Vancouver.What are postulates and theorems in geometryTriangle congruence postulates/criteria (video) | Khan …. We offer tutoring programs for students in K-12, AP classes, and college. SchoolTutoring Academy is the premier educational services company for K-12 and college students. If two sides and the included angle (angle between these two sides) of one triangle are congruent to the corresponding two sides and the included angle of a second triangle, then the two triangles are congruent. Side-Angle-Side Postulate (SAS postulate) If all three sides of a triangle are congruent to corresponding three sides of other triangle then the two triangles are congruent.Īngle-Side-Angle Postulate (ASA postulate)Īccording to this postulate the two triangles are said to be congruent if two angles and the side between these two angles of one triangle are congruent to corresponding angles and the included side (side between two angles) of the other triangle. If the hypotenuse and one of the legs (sides) of a right triangle are congruent to hypotenuse and corresponding leg of the other right triangle, the two triangles are said to be congruent. There are two theorems and three postulates that are used to identify congruent triangles.Īs per this theorem the two triangles are congruent if two angles and a side not between these two angles of one triangle are congruent to two corresponding angles and the corresponding side not between the angles of the other triangle. When triangles are congruent corresponding sides (sides in same position) and corresponding angles (angles in same position) are congruent (equal). Two triangles are said to be congruent if they have same shape and same size.


 0 kommentar(er)
0 kommentar(er)
